Games202-Lecture5 Environment Mapping

SDF

SDF: signed distance field 有向距离场 存储该位置到附近表面的最短距离 正负号代表物体内外

上图为SDF处理软阴影的效果（下面有具体说明）

左图为SDF生成距离场的可视化效果图，在A内部距离为负的涂全黑，在A外部距离越远，颜色越浅。右图为另一种等高线距离场的画法。

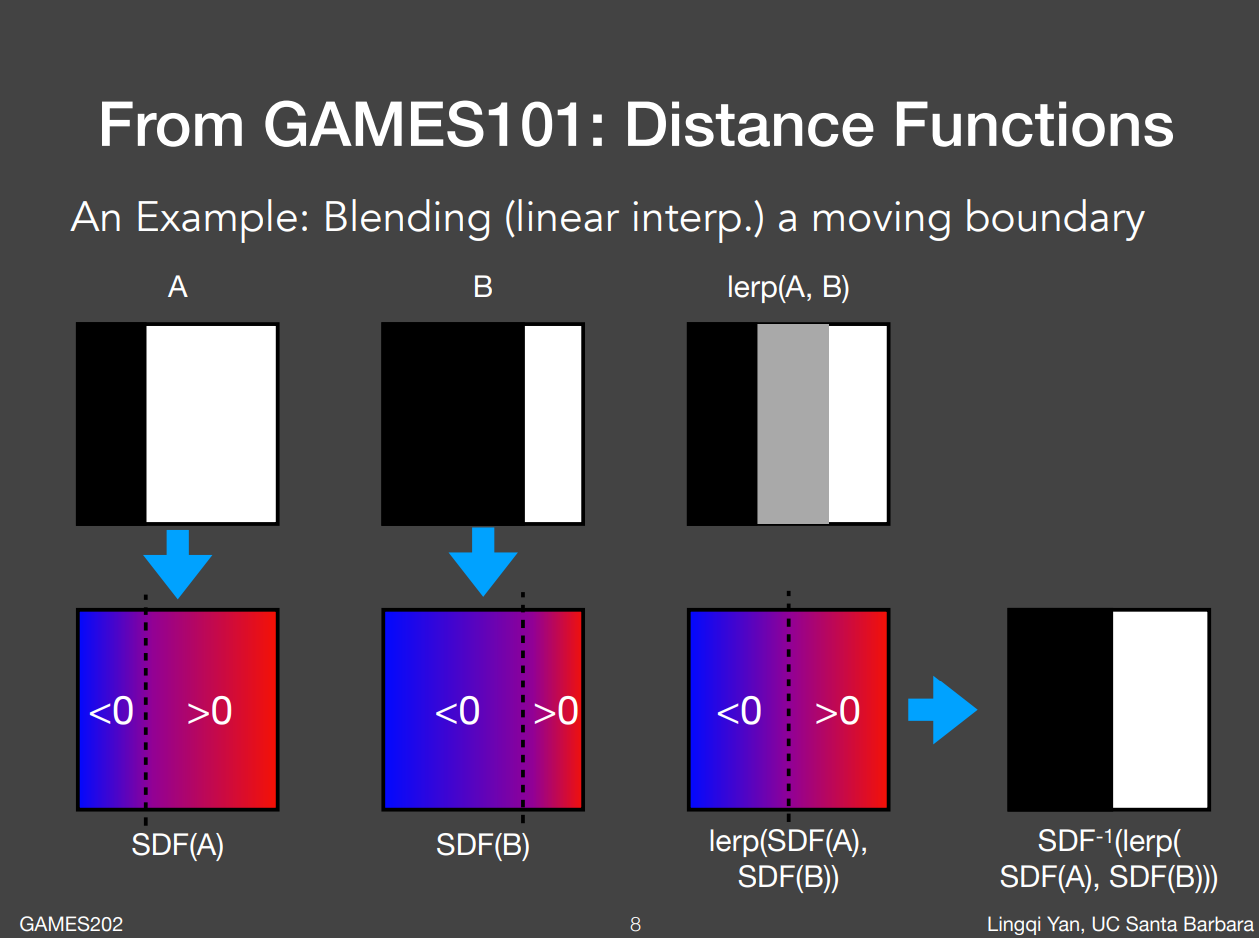
图A中有一个黑色物体向右匀速移动，图B为一段时间后物体的移动位置。现在需要求在中间时刻物体的位置：

​ 1）在101中讲过普通的线性插值方法，对同一个像素的两个不同时间的颜色进行差值，得到的效果为lerp(A,B)。可以看出插值结果为灰色，不符合要求。

​ 2）通过模拟距离场进行差值。黑色内距离为负，白色内距离为正(物体外)。离交界面越远，距离的绝对值越大。此时再次对像素进行距离差值，得到右下图的效果，符合要求。

如图为距离场的另一种应用：物体融合。更详细的理解可以查看"最优传输"技术，在这里不再赘述。

SDF Ray Marching

光线步进(Ray Marching)有时也被称为球体追踪(Sphere Tracing), 因为每次都是检测球形内的物体。使用三维空间内的SDF可以实现最大效率的不定长光线步进。每个SDF存储以该点为球心，距离为半径的球体，球体与最近表面相切且内部一定是空的。因此光线步进的这个半径距离也称为安全距离。

Sphere Tracing 缺点：光线延物体表面步进时步长会特别短，计算量很大；三维SDF需预计算，计算量大，存储信息巨量，且当场景内物体发生形变时更新困难。SDF生成表面不好贴纹理

优化：场景中多个物体可以分别单独计算SDF，整合时每个点取每个物体最小的SDF。

​ 采用类似八叉树的方式进行存储

SDF 生成软阴影

主要思想：通过SDF得到一个大概的 遮挡百分比，用1减去它就得到visibility项

引入安全角度：从地面上的某一shading point向一方向发射一条光线，光线在空中某一点(最小SDF点？)的SDF会构成一个球体。该球体的切线与原始光线的夹角称为安全角度。

渲染阴影时

• safe angle越小，阴影越深。
• safe angle越大，阴影越浅。

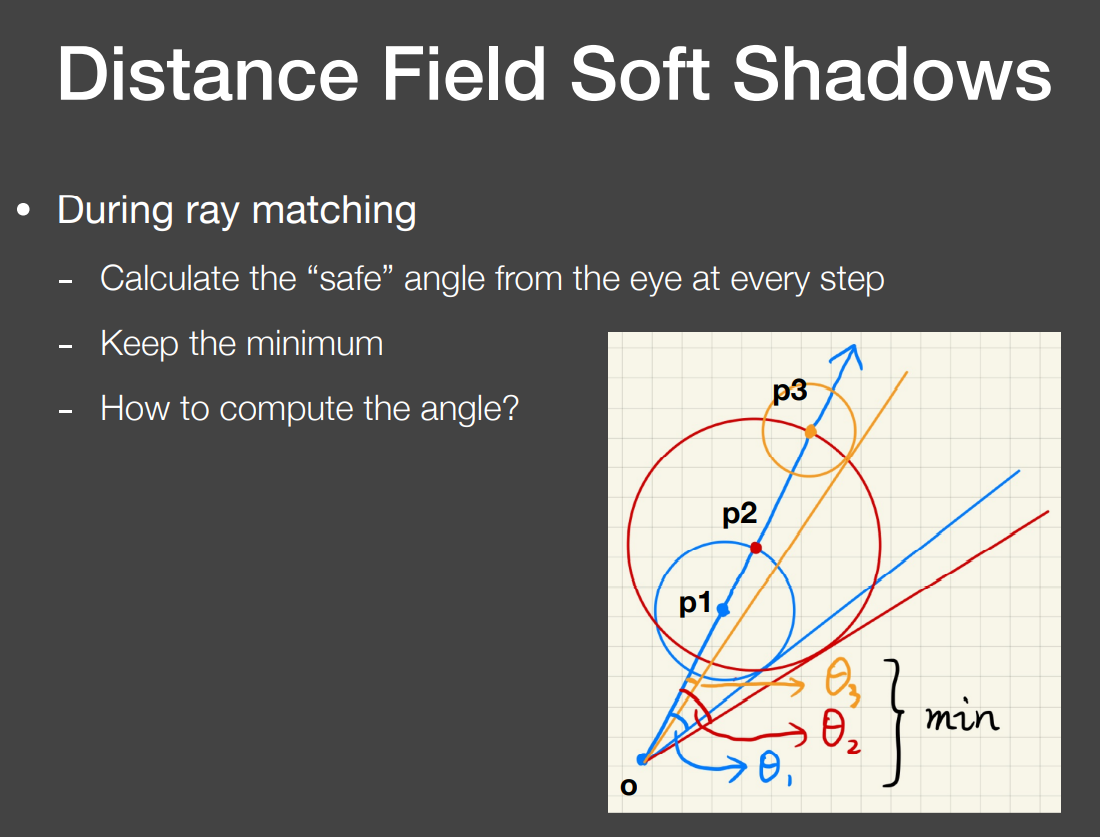
多个遮挡物或多个采样点时，采用之前提到的SDF步进方式，取最小的安全角度为该shading point的软阴影程度。

通常来讲，采用反三角函数的方式可以得到安全角度的值，但是计算量太大、由于可以采用近似方法计算软阴影，即得到的visibility可以不必那么精确。因此直接采用比值的方式求得，大小不超过1。引入系数k来控制阴影的软硬程度。k越小，很大的安全角度也会被纳入阴影之中(只是比较软)；k越大，很小的安全角度也可能算出来的值超过1而被舍弃，不计算阴影。因此k值越大，阴影范围越小，阴影越硬。

Environment Lighting 环境光照

环境光照：使用一张图来存储在场景中向任意方向看去，所获得的光照。假设无限远。

扩展：主流两种存储方式：spherical map与cube map

spherical map：采用球体存储，相机无限远，盲区逐渐收缩成一个点，因此存储的内容为整个环境光照排除一个点。优点：只需要一张贴图；缺点：非线性分布映射，还原困难，中心区域精度最高，四周到背面精度低。

cube map：立方体盒，六个不同方向的贴图合并成一个立方体。使用时立方体中心与光线原点重合，当方向向量向外延伸时，就会和立方体表面上的相应纹理发生相交，我们可以根据该交点结合立方体的方向向量进行采样。

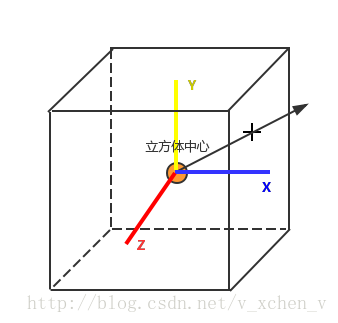
环境光照不需要考虑visibility，从IBL图中可以直接得到shading point 的Li，因此我们的任务就是解渲染方程！

经典解法：蒙特卡洛积分：对于任何积分可以用大量样本进行近似，计算量巨大。因此不太可能用于实时渲染。如何避免sampling(采样)？

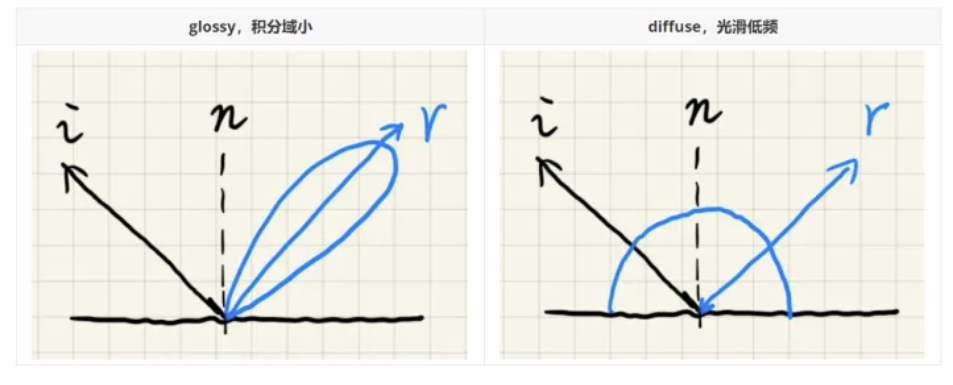
对于两个函数相乘在一定区域内的积分情况，若某个函数在积分区域内分布很均匀或者只在某一小块区域分布，那么可以把另一个函数提出来，积分写成两个积分相乘的形式。 \[ \int_{\Omega} f(x) g(x) d x \approx \frac{\int_{\Omega} f(x) d x}{\int_{\Omega} d x} \cdot \int_{\Omega} g(x) d x \] 当表面为diffuse或者特别specular时，BRDF正好对应化简的两种条件。可以将Li项提出来：

\[ L_o\left(p, \omega_o\right) \approx \frac{\int_{\Omega_{f_r}} L_i\left(p, \omega_i\right) d \omega_i}{\int_{\Omega_{f_r}} d \omega_i} \int_{\Omega+} f_r\left(p, \omega_i, \omega_o\right) \cdot \cos \theta_i d \omega_i \] 提出来的形式可以很明显的发现，右边的式子是BRDF积分，但是左边的式子其实就是对Li在积分区域上取了一个均值。换种说法，就是对材质贴图进行了filter，filter的范围对应的就是积分区域。

因此可以提前对环境贴图做多级的mipmap，不同的等级对应不同的积分区域，越模糊，积分区域越大。

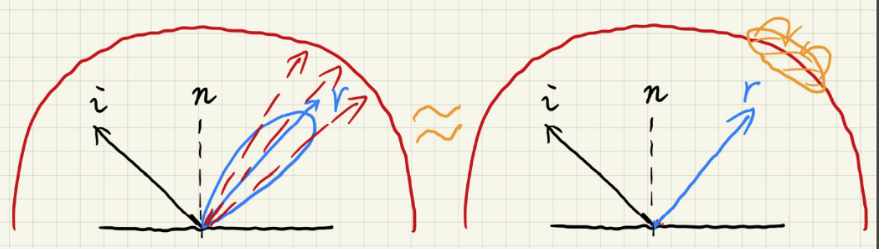
这样做的好处：以前当我们需要计算一个point的某一个lobe波瓣时可能会需要很多分布点进行采样，然后加权平均。现在可以直接取镜面反射的方向上的一个值，mipmap大小根据lobe大小而定。

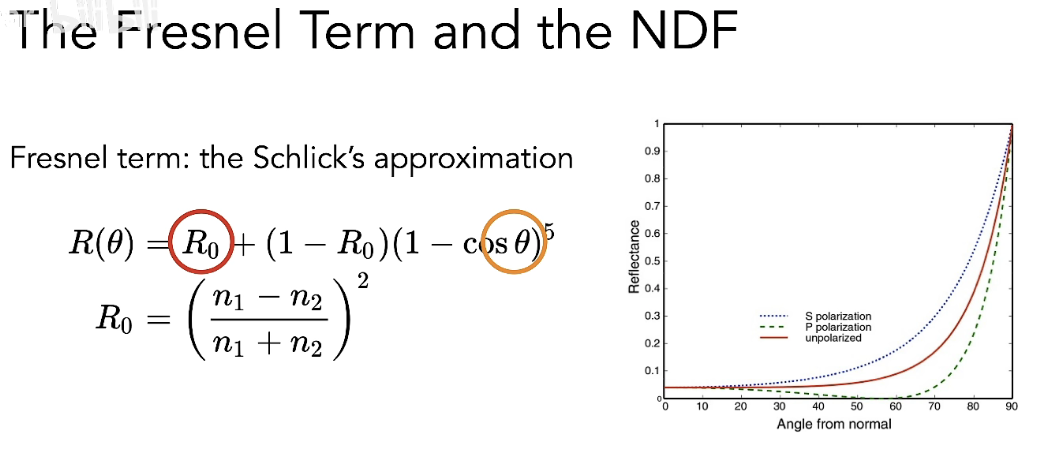
基于以上，我们解决了化简后的BRDF方程乘积的前一项：即环境光照充当入射光，在某一点的入射光如何计算的问题。我们先refilter生成了不同模糊度的环境光照贴图，根据波瓣大小直接使用对应的贴图。那么如何解决后一项BRDF的积分？让我们重新看BRDF的定义： \[ f(\mathbf{i}, \mathbf{o})=\frac{\mathbf{F}(\mathbf{i}, \mathbf{h}) \mathbf{G}(\mathbf{i}, \mathbf{o}, \mathbf{h}) \mathbf{D}(\mathbf{h})}{4(\mathbf{n}, \mathbf{i})(\mathbf{n}, \mathbf{o})} \] F：菲涅尔项。从一个角度看过去，有多少的能量会被反射。因为能量的传播是与入射方向和法线的角度有关的

G：Shadowing-Masking Term。微表面的互相遮挡

D：微表面的法线分布。给定一个入射方向和一个出射方向，可以计算出半程向量h，将h带入半球法线分布中解得在这个点上有多少比例的法线是h方向，作为法线的贡献。因为我们假设只有h方向作为法线才可以实现给定的入射和出射方向的反射。

BRDF的输入很复杂，至少要有入射和出射方向、表面粗糙度等参数，可以进行一波化简：

对F项的化简：

对D项的化简：约等于高斯表面法线正态分布：

不考虑G。综上，BRDF项可以简化为三个输入：R₀，入射角度θ，粗糙度α。（半程向量θ_h可以通过入射角算出来）。

将F项带入渲染方程，将R₀提出来有： \[ \begin{aligned} \int_{\Omega^{+}} f_r\left(p, \omega_i, \omega_0\right) \cos \theta_i \mathrm{~d} \omega_i \approx & R_0 \int_{\Omega^{+}} \frac{f_r}{F}\left(1-\left(1-\cos \theta_i\right)^5\right) \cos \theta_i \mathrm{~d} \omega_i+ \\ & \int_{\Omega^{+}} \frac{f_r}{F}\left(1-\cos \theta_i\right)^5 \cos \theta_i \mathrm{~d} \omega_i \end{aligned} \] R₀其实就是base color，或者说是albedo或者反照率。这样做就把BEDF对于R₀的依赖消去了。这样的话BRDF就变成二维输入了：入射角度θ，粗糙度α。可以直接将其打表，写成一张二维的texture：

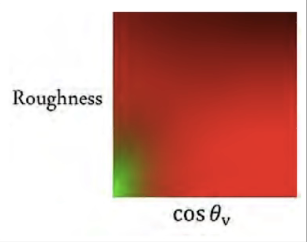
工业界就是利用以上的方式将渲染方程拆分之后分别求解。Li项通过mipmap在反射方向直接采样。BRDF项通过查表获得。 \[ \frac{1}{N} \sum_{k=1}^N \frac{L_i\left(\mathbf{l}_k\right) f\left(\mathbf{l}_k, \mathbf{v}\right) \cos \theta_{\mathbf{l}_k}}{p\left(\mathbf{l}_k, \mathbf{v}\right)} \approx\left(\frac{1}{N} \sum_{k=1}^N L_i\left(\mathbf{l}_k\right)\right)\left(\frac{1}{N} \sum_{k=1}^N \frac{f\left(\mathbf{l}_k, \mathbf{v}\right) \cos \theta_{\mathbf{l}_k}}{p\left(\mathbf{l}_k, \mathbf{v}\right)}\right) \] 以上就是split sum的原理。